Digital signatures, which are covered in another section, use elliptical curve mathematics. Elliptical curves allow one person to choose a starting point and then perform a one way operation to create a second point such that it is it not possible to find the first point from the finial derived point.
Using elliptical curve functions, students can actually draw their own graphs, chose their points, and derive a final point to see how this cryptography works under the hood.
By doing this, students take advanced mathematics and real world application to gain an understanding much deeper than numbers and computation. They can gain an understanding of the security of the digital functions they use on their very smart phones and websites.
Learn more with resources found in the Bitcoin Classroom Library:
Knutson, Hans. “What Is the Math behind Elliptic Curve Cryptography?” Hacker Noon, Hacker Noon, 7 Apr. 2018, hackernoon.com/what-is-the-math-behind-elliptic-curve-cryptography-f61b25253da3.
This article on Hacker Noon describes in detail how the math behind elliptical curves works in cryptography.
Level: Intermediate
“Elliptic Curve Cryptography: a Gentle Introduction.” Andrea Corbellini Atom, andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/.
Andrea describes this as “a gentle introduction” but I don’t think it is, which means that the concept explanations can get a lot deeper!
Level: Advanced
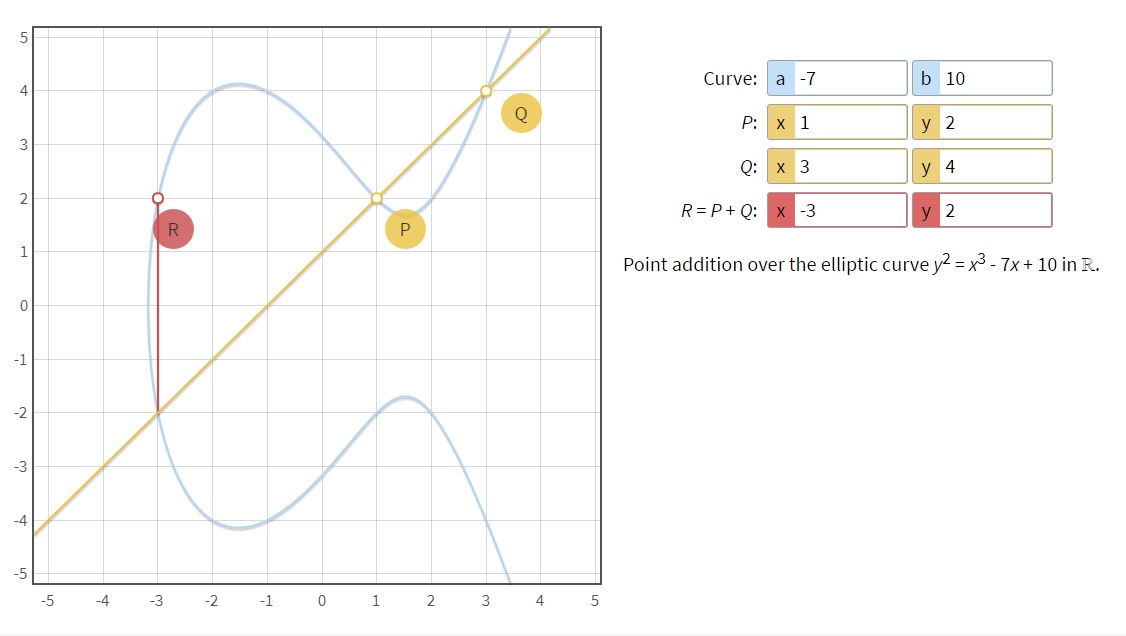
Elliptic Curve Point Addition (ℝ), cdn.rawgit.com/andreacorbellini/ecc/920b29a/interactive/reals-add.html.
This is an interactive elliptical curve addition tool.
Oleganza. “ELI5: How Digital Signatures Actually Work.” Oleg Andreev, 11 July 2017, blog.oleganza.com/post/162861219668/eli5-how-digital-signatures-actually-work.
This is simplest explanation of how digital signatures work on a technical level.
Level: Beginner
